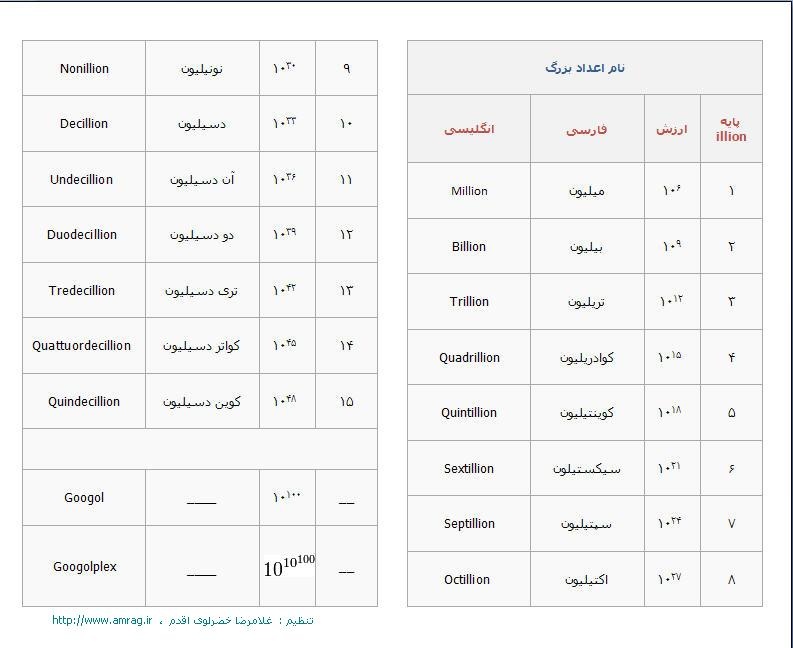
انجمن علمی و آموزشی معلمان ریاضی استان آذربایجان غربی
.: ریاضیات شانه بر زلف پریشان عالم است :.
انجمن علمی و آموزشی معلمان ریاضی استان آذربایجان غربی
.: ریاضیات شانه بر زلف پریشان عالم است :.. اعداد خوشحال!
عدد صحیح مثبتی را در نظر بگیرید ، مجموع مربعات ارقام آن را به عنوان عدد بعدی بنویسید و این کار را ادامه دهید .
در صورتیکه این رویه به عدد یک ختم شود ، عدد اصلی شما یک عدد خوشحال یا happy number نامیده می شود ، در غیر این صورت آن عدد یک عدد غیر خوشحال یا unhappy number می باشد .
به طور مثال :
۷ -> ۴۹ -> ۹۷ -> ۱۳۰ -> ۱۰ -> ۱ پس عدد ۷ یک عدد خوشحال است
۴ -> ۱۶ -> ۳۷ -> ۵۸ -> ۸۹ -> ۱۴۵ -> ۴۲ -> ۲۰ -> ۴ پس عدد ۴ یک عدد غیر خوشحال است
تعریف : عدد معلوم n = n۰ را در نظر گرفته و دنباله ای از اعداد ... , n۱ , n۲ , n۳ را تعریف می کنیم به طوریکه ni+۱ مجموع مربعات ارقام ni باشد . آنگاه n یک عدد خوشحال است ، اگر و تنها اگر وجود داشته باشد i ی که ۱ =ni
اگر عددی خوشحال باشد تمام اعضای دنباله آن نیز خوشحال خواهند بود و همچنین اگر عددی غیر خوشحال باشد تمام اعداد دنباله آن غیر خوشحال می باشند . ۷ یک عدد خوشحال است ، پس اعداد حاصل از آن در دنباله همگی اعداد خوشحال هستند .
۴۹ = ۷۲
۹۷ = ۹۲ + ۴۲
۱۳۰ = ۷۲ + ۹۲
۱۰= ۰۲ + ۳۲ + ۱۲
۱ = ۰۲ + ۱۲
و همچنین اگر ارقام آن را جابهجا کنیم عدد حاصل باز عدد خوشحال است .
اعداد خوشحال کمتر از ۵۰۰ عبارتند از :
1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100, 103, 109, 129, 130, 133, 139, 167, 176, 188, 190, 192, 193, 203, 208, 219, 226, 230, 236, 239, 262, 263, 280, 291, 293, 301, 302, 310, 313, 319, 320, 326, 329, 331, 338, 356, 362, 365, 367, 368, 376, 379, 383, 386, 391, 392, 397, 404, 409, 440, 446, 464, 469, 478, 487, 490, 496.
عدد اول خوشحال ، عدد خوشحالی است که عدد اول باشد .
همه اعداد و در نتیجه همه اعداد اول به شکل ۳ + ۱۰n و ۱۰n + ۹ برای nهای بزرگتر از ۰ اعداد خوشحال هستند .
به عنوان مثال ، برای اولی عدد ۱۳ و برای دومی عدد ۱۹ را می توان در نظر گرفت .
برای کسب اطلاعات بیشتر اینجا کلیک کنید .
گروه ریاضی ناحیه ۲
رقیه نامور
از خانم نامور به خاطر ارسال مقاله متشکریم
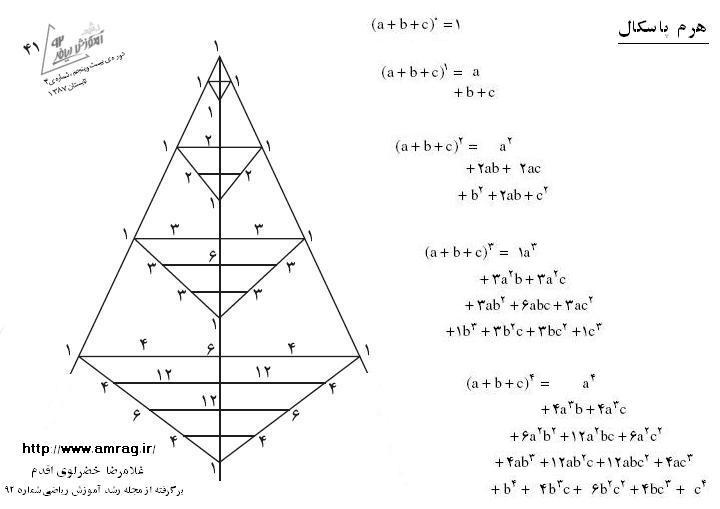
. هرم پاسکال
عکس زیر با جزئی تغییر ، قسمتی از مقاله ای با عنوان هرم پاسکال است که توسط رباب حدادیان همکار ریاضی از شهرستان زنجان نوشته شده و در شماره ۹۲ مجله رشد آموزش ریاضی بچاپ رسیده است .
علاقه مندان برای دریافت این مقاله می توانند اینجا کلیک کنند و در صفحه باز شده از ردیف ۸ ، آن را دانلود نمایند .
. فرما و آخرین قضیه او
پس از درگذشت فرما، فرزندش ساموئل کار انتشار آثار او را به عهده گرفت. ساموئل، ضمن جمع آوری نوشته های پدرش، کتابها و مقالات مورد مطالعه وی را نیز بررسی نمود و همین امر باعث انتشار قضیه معروف فرما شد. او دریافت که پدرش، 48 نظر تحت عنوان «نظریات روی کتاب دیوفانتس» نوشته است. در هشتمین مساله، آنچه که بعدها به آخرین قضیه فرما مشهور گردید، بیان شده بود. این مساله به زبان نمادین به این صورت است: برای هر عدد صحیح n>2 معادله ی an + bn = cn فاقد جواب صحیح مثبت است. فرما ادعا کرده بود که روشی شگفت انگیز برای اثبات این مطلب یافته است، اما حاشیه کتاب باریکتر از آن است که آن را در خود جای دهد! هر حدس یا قضیه ی دیگری که فرما به این روش اعلام کرده بود تا سال 1847 اثبات شد، مگر آخرین آنها که همین قضیه باشد.اکنون که بیش از سه قرن از درگذشت فرما می گذرد، کارهای او در غیر از نظریه اعداد، اهمیت خود را در ذهن افراد از دست داده است. البته دلیل این مطلب آن است که کارهای وی قدمهای اولیه ی اساسی در توسه ی نظریات مهمی بوده که امروزه کاملا فهمیده شده اند و به راحتی با زبان نمادین ریاضی –که در زمان فرما موجود نبوده- قابل بیانند. علاقه عمیق فرما به نظریه اعداد از گفته ی وی که مطالعه خواص اعداد صحیح مثبت، بزرگترین عرصه قدرت نمایی استدلال ریاضی محض و بزرگترین گنجینه حقایق ریاضی محض است پیداست. قضیه فرما، پیش از قرن بیستم – میدانهای اقلیدسی اعداد در 4 آگوست 1753 اویلر در نامه ای به گلدباخ، ادعا کرد که قضیه فرما را در حالت N=3 ثابت کرده است. البته اثلات وی اشتباه جالبی داشت. او به دنبال یافتن مکعب هایی از فرم بود... فرد دیگری که قدمی به جلو برداشت، سوفی ژرمن بود. او نشان داد که اگر n و 2n+1 اعداد اولی باشند، آنگاه ایجاب می کند که یکی از x،y یا z بر n بخشپذیر باشد. بنابراین قضیه آخر فرما به دو حالت زیر تفکیک می شود: (1) n هیچیک از x و y و z را نمی شمارد. (2) n یکی از x و y و z را می شمارد. سوفی ژرمن حالت (1) را برای هر n<100 ثابت کرد و لژاندر روش وی را به همه ی اعداد کوچکتر از 197 گسترش داد. حالت (2) برای n=5 به دو بخش تقسیم شد و بخشی را دیریکله در جولای 1825 و حالت دیگر را لژاندر در سپتامبر 1825 ثابت کرد. در سال 1832 دیریکله اثباتی از قضیه فرما را برای n=14 منتشر کرد. حالت n=7 در 1839 توشط لامه ثابت شد.سال 1847 در مطالعه قضیه فرما اهمیت زیادی داشت. در اول ماه مارس 1847 لامه ادعا کرد که قضیه آخر فرما را ثابت کرده است. این ادعای لامه عملا منجر به پیشرفتهایی در مبحث میدانهای اقلیدسی اعداد شد. قضیه فرما در قرن بیستم با وجود جوایزی که برای حل مساله فرما گذاشته شده بود، این قضیه، همچنان حل نشده باقی ماند و رکورددار بیشترین اثباتهای غلط شد. مثلا بیش از 1000 اثبات غلط در بین سالهای 1908 تا 1912 منتشر گردید. کومر با معرفی مفاهیم عمده ای در نظریه اعداد مانند اعداد سیکلوتومیک، یکتایی تجزیه و عدد رده ای توانست قضیه فرما را برای n های اول کمتر از 100 بجر 37 و 56 و 67 – که به اصطلاح اعداد نامنظم (irregular) بین یک و صد نامیده می شوند – ثایت کند. در سال 1857 کومر قضیه فرما را برای این اعداد نیز ثابت کرد. البته اثبات او نقص هایی داشت که در سال 1920 ون دیور آنها را برطرف نمود. نتیجه های فوق برای n های خاص بوده است. در این باره تا سال 1992 درستی آخرین قضیه فرما برای همه ی اعداد اول n<4000000 به کمک کامپیوتر بدست آمد. اولین کار عمده برای n دلخواه، در قرن بیستم، در اوایل دهه 1980 توسط فالتینگز انجام شد. وی حدس موردل را که در سال 1922 مطرح شده بود ثابت کرد. این حدس به قرار زیر است: «تعداد نقاط گویا روی یک منحنی با ضرایب گویا و گونای بزرگتر یا مساوی دو، متناهی است. علت ارتباط این مساله با قضیه ی فرما این است که هر جواب صحیح و غیر صفر مانند x و y و z برای معادله ی متناظر است با یک نقطه با مختصات گویا روی منحنی و برعکس.اما این ارتباط در نهایت حاصلی برای اثبات قضیه آخر فرما نداشت. البته اثبات حدس موردل توسط فالتینگز با معرفی ایده های جدیدی همراه بود که باعث توسه ی مفاهیم اساسی در هندسه جبری حسابی گردید. فصل آخر داستان فصل پایانی داستان قضیه آخر فرما در سال 1955 آغاز گردید. یوتاکا تانیاما آغازگر این حرکت اساسی بود. وی در سال 1927 در منطقه ای در شمال توکیو متولد شد و در سال 1953 از دانشگاه توکیو در «نظریه جبری اعداد» فارغ التحصیل گردید. او کتاب «نظریه اعداد مدرن» را همراه شیمورا در سال 1957 نوشت. با اینکه آینده ی بزرگی، به ویژه از نظر علمی برای تانیاما متصور می شد، او در روز 17 نوامبر 1958 در توکیو خودکشی کرد. تانیاما به عنوان دلیل خودکشی خود نوشته است: «تا دیروز دلیلی قطعی برای کشتن خود نداشتم... خودم هم نمی فهمم، اما این نتیجه ی اتفاق یا موضوع خاصی نیست.»حدود یک ماه بعد دختری که تانیاما قصد ازدواج با او را داشت نیز خودکشی کرد! تانیاما سوالاتی درباره ی خمهای بیضوی – یعنی خم هایی بفرم پرسید. کارهای بیشتر که در این زمینه توسط ویل و شیمورا انجام شد، حدسی را بوجود آورد که به حدس شیمورا-تانیاما-ویل مشهور گردید. این حدس حاکی است که هر خم بیضوی را که بر اعداد گویا تعریف می شود، می توان به وسیله ی توابع پیمانه ای بیضوی، پارامتری کرد.در سال 1986، ارتباطی بین حدس شیمورا-تانیاما-ویل و قضیه ی آخر فرما توسط فری و سر ایجاد شد. در همهن دهه دهه کن ریبت، بر اساس کارهای انجام شده توسط سر، نشان داد که قضیه آخر فرما از حدس شیمورا-تاناما-ویل نتیجه می شود. اندرو وایلز و اثبات قضیه آخر فرما اندر جان وایلز (Andrew John Wiles) در 11 آوریل 1953 در کمبریج انگلستان به دنیا آمد. علاقه ی او به قضیه ی فرما زمانی که او کودکی ده ساله بود شکب گرفت. او در این باره می گوید: «من ده ساله بودم که روزی در کتابخانه ای عمومی یک کتاب ریاضی پیدا کردم. در این کتاب مطالب تاریخی بسیاری درباره ی مساله ای آمده بود. من در حالی که فقط ده سالم بود، صورت آن مساله را فهمیدم و سعی کردم آن را ثابت کنم. مساله ی جالبی بود. این مساله همان قضیه ی آخر فرما بود!» وایلز درجه دکترای خود را از دانشگاه کمبریج دریافت نمود. استاد راهنمای وی در کمبریج جان کوتز بود. وی درباره ی وایلز گفته است: «من از داشتن دانشجویی مثل اندرو خیلی خوشحال بوده ام. او ایده های عمیقی در تحقیقات داشت و همیشه واضح بود که ریاضیدانی خواهد شد که کارهای بزرگی انجام می دهد!» اندرو وایلز در دهه 1980 به دانشگاه پرینستون رفت. وی پس از شروع کار روی قضیه فرما تقریبا تحقیقات دیگرش را کنار گذاشت. خود وایلز در این باره گفته است که بعد از مدتی متوجه شده که صحبت کردن با دیگران درباره ی قضیه فرما غیر ممکن است. زیرا این مطلب به موضوع شدیدا جالب توجهی برای همه تبدیل شده! تنها کسی که از کار کردن وایلز روی قضیه آخر فرما اطلاع داشت، همسرش بود. وایلز در این باره گفته است: «فقط همسرم می دانست که من روی قضیه فرما کار می کنم. من بعد از گذشت چند روز از ازدواجمان به او گفته بودم که قصد دارم روی این قضیه کار کنم...» وایلز دقیقه های هفت سال اول کارش روی این قضیه را بسیار پرارزش، مورد علاقه و سخت توصیف نموده و گفته است که قطعا نمی خواهد چنین کاری را تکرار کند. وی نهایتا در سال 1994 به اثبات حالت خاصی از حدس شیمورا-تانیاما-ویل و استنتاج قضیه آخر فرما موفق شد. وایلز در این باره می گوید: «... این مهمترین لحظه ی زندگی کاری من بود. چیزی که ممکن است هرگز دوباره تکرار نشود! ... پس از اتمام کار، حدود بیست دقیقه گیج بودم. سپس در طول روز در دانشکده قدم می زدم. وقتی به پشت میزم برگشتم، آنرا همانجا دیدم! هنوز همانجا بود !! ...» مقاله ای که وایلز در آن قضیه آخر فرما را ثابت کرده «خمهای بیضوی و پیمانه ای و قضیه آخر فرما» نام دارد، که در سال 1995 منتشر شد. سیل تبریک ها و جوایز مختلف از سال 1995 به بعد به سوی او جاری شد، در حالی که در طول سالها تلاشش برای اثبات قضیه فرما، به خاطر ترک تحقیقات دیگر و کمرنگ شدن کارش مورد سرزنش و مواخذه قرار گرفته بود !! شاید آرزوی بسیاری از دانشجویان جوان ریاضی مطالعه و فهمیدن اثبات قضیه ای باشد که صورتی بدین سادگی و اثباتی آنچنان پرماجرا داشته است. منبع : دانش ما |
. رابطه ریاضی فاصله سیارات تا خورشید
رابطه ریاضی فاصله سیارات تا خورشید
سال ۱۷۶۶ میلادی، یوهان تیتوس منجم آلمانی توانست رابطه ساده ای بیابد که با استفاده از آن می شد فاصله سیارات از خورشید را بدست آورد. چند سال بعد نیز دیگر منجم هموطن او، یوهان الرت بفد، این رابطه را مستقلا” دوباره کشف کرد.البته این رابطه را هر دو از طریق بازی با اعداد بدست آوردند و بدست آوری آن رابطه پایۀ علمی نداشت. امروزه این رابطه به رابطه تیتوس_بفد مشهور است. این رابطه بدین صورت است:
فاصله سیاره از خورشید (بر حسب فاصله متوسط زمین از خورشید) = ۴ / ۰ + ( ۳ / ۰ n x )
... , n = ۰ , ۱ , ۲ , ۴ , ۸
اعداد بدست آمده با دقت خوبی با فاصله واقعی سیارات همخوانی داشت:

برای فاصله ۲.۸ برابر فاصله زمین از خورشید در آن زمان سیاره ای یافت نشده بود. بسیاری از اخترشناسان عقیده داشتند که سیاره ای کوچک در این فاصلۀ بین مریخ و مشتری وجود دارد که کشف نشده است. جستجوی منظم نوار دایرةالبروج برای یافت این سیارۀ مفقود از اواخر قرن هجدهم شروع شد و سرانجام در اولین روز قرن نوزدهم، یک منجم ایتالیایی به نام جوزپه پیاتزی، موفق شد جسم کوچکی را در حدود این فاصله از خورشید بیابد که آن را سفرفس نامید. بعد از آن نیز اجرام دیگری با همین فاصله از خورشید کشف شدند. اخترشناسان آن دوران این نظریه را پیش کشیدند که در آن فاصله از خورشید، بجای یک سیاره، تعداد زیادی سیارک وجود دارد که با کشف تعدادزیادی از این سیاکها در سالهای بعد این نظریه تایید شد.در حقیقت رابطه تیتوس_بفد محرک اصلی کشف سیارکها بود.
سالها بعد نیز سیارۀ اورانوس کشف شد که فاصله اش با فاصله پیشبینی شده توسط رابطه تیتوس_بفد نیز می خواند!(۱۹.۶ بنابر رابطه و ۱۹.۹ بنابر اندازه گیری). اما فاصله سیارات بعدی نپتون و پلوتو در این رابطه صدق نمی کنند. امروزه نظریه ای که به نظریه واهلش دینامیکی(Dynamical Relaxation) موسوم است توضیحی برای این رابطه یافته است. بنا به این نظریه، سیارات نخست در مدارات متفاوت تکوین یافتند؛ اما سپس به مداراتی منتقل شدند که نیروهای اغتشاشی گرانشی دیگر سیارات را به حداقل برسانند. نتیجه این کار از نظر ریاضی به روابطی شبیه رابطه تیتوس_بفد منجر می شود.
. اعداد تاکسی!
زمانی که ریاضیدان انگلیسی هاردی برای عیادت ریاضیدان شهیر هند رامانوجان به بیمارستان رفته بود به
این موضوع اشاره کرد که شماره تاکسی که به وسیله آن به بیمارستان آمده ، عدد بی ربط و بی خاصیت
۱۷۲۹ بوده است .
رامانوجان بلافاصله ضمن رد ادعای هاردی به او یادآور شد که اتفاقا ۱۷۲۹ بسیار جالب توجه است .
خود ۱۷۲۹ عدد اول است .
دو عدد ۱۷ و ۲۹ هر کدام عدد اول هستند .
جمع چهار رقم تشکیل دهنده آن میشود ۱۹ که عدد اول است .
جمع دو عدد اولیه و دو عدد آخری میشود ۸۱۱ که باز هم عدد اول است .
دو عدد ابتدایی(سمت چپ) اگر جمع شوند؛عدد ۸۲۹ میشود که باز هم عدد اول است .
دو عدد اولیه اگر از هم دیگر کسر شوند؛عدد ۶۷ ساخته میشود که باز هم عدد اول است .
سه عدد سازنده آن عدد اول است (۱ و ۷ و ۲) .
جمع اعداد تشکیل دهنده ۱۷۲۹ برابر ۱۹=۹+۲+۷+۱ است ؛ عکس عدد ۱۹ عدد ۹۱ است ؛ اگر ۱۹ در ۹۱
ضرب شود ، حاصل برابر ۱۷۲۹ می شود . این هم یکی دیگر از اختصاصات عدد ۱۷۲۹ است که در هر عددی
دیده نمی شود .
عدد ۱۷۲۹ اولین عددی است که می توان آنرا به دو طریق به صورت حاصلجمع مکعبهای دو عددمثبت نوشت:
۱۲ به توان ۳ + ۱ به توان ۳ و ۱۰ به توان ۳ + ۹ به توان ۳ هر دو برابر ۱۷۲۹ می باشند .
اولین مطلب موجود در رابطه بااین خاصیت ۱۷۲۹به کارهای بسی ریاضیدان فرانسوی قرن هفدهم بازمی گردد.
حال اگر کمی مانند ریاضیدانها عمل کنید باید به دنبال کوچکترین عددی بگردید که به سه طریق مختلف
حاصلجمع مکعبهای دو عدد مثبت است این عدد ۸۷۵۳۹۳۱۹ می باشد که در سال ۱۹۵۷ توسط لیچ کشف
شد : ۴۱۴ به توان ۳ + ۲۵۵ به توان ۳ و ۴۲۳ به توان ۳ + ۲۲۸ به توان ۳ و ۴۳۶ به توان ۳ + ۱۶۷
به توان ۳ هر سه جوابشان برابر ۸۷۵۳۹۳۱۹ است .
امروزه ریاضیدانان عددی را که به n طریق مختلف به صورت حاصلجمع مکعبهای دو عددمثبت باشد ، n ــامین
عدد تاکسی می نامند و آنرا با Taxicab Number نمایش می دهند.
جالبتر از همه اینکه ، هاردی و رایت ثابت کردند برای هر عدد طبیعی n نا کوچکتر از 1، n ــامین عدد تاکسی
وجود دارد!
هرچند،چهارمین تا هشتمین اعداد تاکسی نیز کشف شده اند ولی تلاشها برای یافتن نهمین عدد تاکسی
تاکنون ناکام مانده است . متاسفانه اطلاعات زیادی درباره اعداد تاکسی موجود نیست .
در ضمن می توان مسئله را از راههای دیگر نیز گسترش داد.مثلا همانگونه که هاردی در ادامه داستان فوق
از رامانو جان پرسید و او قادر به پاسخگویی نبود، این پرسش را مطرح کنید: کوچکترین عددی که به دو طریق
حاصلجمع توانهای چهارم دو عدد مثبت می باشد ، کدام است؟
جواب این سئوال عدد ۶۳۵۳۱۸۶۵۷ می باشد ، این عدد توسط اویلر پیدا شده است . عدد ۶۳۵۳۱۸۶۵۷
حاصلجمع توانهای چهارم ۵۹ و ۱۵۸ و همچنین حاصلجمع توانهای چهارم ۱۳۳ و ۱۳۴ می باشد .
برای کسب اطلاعات بیشتر به آدرس های زیر مراجعه نمائید :
http://en.wikipedia.org/wiki/Taxicab_number ، http://mathworld.wolfram.com/TaxicabNumber.html
. اضطراب ریاضی
هدف این مقاله بررسی اثر بخشی حالت های عاطفی و هیجانی ، به عنوان مولفه های شخصیت یادگیرنده بررفتار ریاضی است. امروزه اضطراب ریاضی مورد توجه و علاقه بسیاری از متخصصان روان شناسی آموزش ریاضی و نیز روانشاسان شناختی است تا از این طریق تأثیرهای هیجانی و بر انگیختگی های روانی شاگردان را در کار ریاضی بشناسند و برای کنترل و مهارعلمی آنها راه کارهای عملی بیابید . در این میان اضطراب و فشار روانی و تعامل آنها با یادگیری ریاضیات جایگاه ویژه ای را در امر آموزش و یادگیری ریاضیات مدرسه و حتی دانشگاهی به خود اختصاص داده است ؛ هر چند که در محافل علمی و آموزشی ما کمتر به آن توجه شده است.
ادامه مطلب .... فراکتال و نظریه آشوب
فراکتال و نظریه آشوب
شاید تا کنون بارها نام فراکتالها یا برخالها را شنیده باشید؛ موجوداتی که به عنوان اصلی ترین بازیگران هندسه منتج از نظریه آشوب شناخته می شوند.
این هندسه ویژگی های منحصر به فردی دارد، که می تواند توجیه گر بسیاری از رویدادهای جهان اطراف ما باشد، اما ویژگی اصلی که در تعریف آشوب و بالطبع هندسه آن وجود دارد، باعث می شود ما استفاده ویژه ای از این سیستم ببریم.
این روزها از فراکتالها به عنوان یکی از ابزارهای مهم در گرافیک رایانه ای نام می برند، اما هنگام پیدایش این مفهوم جدید بیشترین نقش را در فشرده سازی فایلهای تصویری بازی کردند.
برای آن که درک بهتری نسبت به فراکتالها داشته باشیم ، بد نیست نگاه مختصری به آشوبی بیندازیم ، که فراکتال ها فضای هندسی آنها را تعریف می کند.
. مثلث عروس!
هزاران سال پیش ، مصریان در سرزمین باستانی خود که مهد تمدن بود ؛ در کنار رود نیل ، کشاورزی می کردند . آن ها کاخ های عظیمی در این سرزمین ساخته اند .
آیا اهرام مصر را دیده اید؟ آیا می دانید مصریان باستان ، چگونه گوشه های این بناهای عظیم را قائمه ساخته اند؟ آیا باور می کنید که آن ها این کار را به کمک یک ریسمان انجام داده باشند؟
مصریان با 11 گره، ریسمان را به 12 قسمت برابر تقسیم می کردند. دو سر ریسمان را به هم گره میزدند. در محلی که می خواستند زاویه ی قائمه بسازند، یک میخ می کوبیدند. یک گره ریسمان را به پشت این میخ می انداختند، سپس سه گره می شمردند و ریسمان را می کشیدند تا صاف شود. گره سوم را با میخ به زمین ثابت می کردند. دوباره سراغ گوشه ی زمین می رفتند؛ این بارچهار گره از طرف دیگر می شمردند. ریسمان را صاف می کردند و گره چهارم را به زمین ثابت می کردند.
کاری که مصریان باستان انجام می دادند، در اصل ، ساختن یک مثلث بود. طول ریسمان در دو طرف گوشه ی زمین، سه قسمت و چهار قسمت و در مقابل پنج قسمت بود. امروزه ما میدانیم مثلثی که اضلاع 3و4و5 داشته باشد، طبق عکس رابطه ی فیثاغورس ، مثلث قائم الزاویه است.
در گذشته این مثلث، به مثلث عروس معروف بوده است
. قدرت اعداد
در گذشته های دور، یکی از پادشاهان هندوستان به ازای یاد دادن سرگرمی خوبی به او، جایزه بزرگی تعیین کرد. می دانید که هندی ها در ابداع و اختراع روابط شگفت انگیز بین اعداد بسیار توانا هستند و تاریخچه بلندی در این زمینه دارند.
روزی یکی از همین دانشمندان متبحر کار با اعداد، نزد پادشاه رفت و بازی شطرنج را به او آموخت. کسی چه می داند، شاید بازی شطرنج از همان زمان اختراع شده باشد.این مرد زیرک به ازای سرگرمی خوبی که به پادشاه آموخته بود از وی خواست تا به ازای ۶۴ خانه شطرنج به او گندم دهد. بدین ترتیب که از یک دانه گندم برای خانه اول آغاز کند و به هر خانه شطرنج که رسید تعداد دانه های گندم را نسبت به خانه قبل دو برابر افزایش دهد. مثلاً برای روز چهارم پادشاه می بایست تعداد ۱۶=4^2 دانه گندم به مرد فاضل بدهد. مرد خردمند شرط کرد که در صورت عدم توانایی پرداخت این گندم ها از سوی پادشاه می باید تاج و تخت هندوستان را برای همیشه ترک کند. پادشاه نیز با کمال میل پذیرفت و در دل به بی خردی آن ناشناس خندید.
مسلماً در روزهای اول مشکلی وجود نداشت. اما مشکل اصلی از آنجا شروع می شد که این اعداد به صورت شگفت آوری بزرگ می شدند. در روز دهم تعداد ۱۰۲۴=10^2 دانه گندم باید پرداخت می شد که تعداد زیادی نیست. اما روز بیستم تعداد قابل ملاحظه ای می شود یعنی ۵۷۶/۰۴۸/۱=20^2 دانه گندم. فکر می کنید وقتی که به روز آخر یعنی خانه شصت و چهارم برسید چه اتفاقی بیفتد. درست حدس زده اید پادشاه ما به ….=64^2 دانه گندم نیاز دارد که این تعداد گندم با تمام دانه های شن و ماسه موجود بر روی زمین برابری می کند! در روزهای آخر این شرط تازه پادشاه هند متوجه شد که چه کلاه بزرگی سرش رفته است اما چاره ای جز کناره گیری از تاج و تخت نبود!مثال های بسیاری از این دست موجود است که به قدرت شگرف اعداد و بیشتر از آن به قدرت تفکر انسان هایی که راه سود بردن از آن را بدانند اشاره می کند.
. چرا ریاضیات می خوانیم؟
چرا باید ریاضیات بخوانیم؟راجر بیکن، فیلسوف انگلیسی در سال 1267 میلادی پاسخ این سوال را این چنین داده است: «کسی که این کار را نکند نمی تواند چیزی از بقیه علوم و هر آن چه در این جهان هست بفهمد . . . چیزی که بدتر است این است که کسانی که ریاضیات نمی دانند به جهالت خودشان پی نمی برند و در نتیجه در پی چاره جویی برنمی آیند.» می توانم همین جا سخن را پایان دهم اما ممکن است بعضی ها فکر کنند که شاید خیلی چیزها در هفت قرن گذشته تغییر کرده باشد.
شاهدی تازه می آورم، پال دیراک از خالقان مکانیک کوانتومی، معتقد است که وقتی تئوری فیزیکی ای را پایه ریزی می کنید نباید به هیچ شهود فیزیکی اعتماد کنید. پس به چه چیزی اعتماد کنید؟ به گفته این فیزیکدان مشهور، فقط به برنامه ای متکی بر ریاضیات ولو این که در نگاه اول ربطی به فیزیک نداشته باشد.در حقیقت، در فیزیک تمامی ایده های صرفا فیزیکی رایج در ابتدای این قرن کنار گذاشته اند در حالی که الگوهای ریاضی ای که به زرادخانه های فیزیکدان ها راه یافته اند به تدریج معنای فیزیکی یافته اند. در این جاست که قابل اعتماد بودن ریاضیات به روشنی رخ می نمایاند. بنابراین الگو سازی ریاضی روشی پربار برای شناخت در علوم طبیعی است .
موریس کلاین می نویسد: یونانی های قدیم واقعیت های دنیای اطراف خود را با علم ریاضیات منطبق می دیدند و حقیقت نمایی طرح کیهان را در ریاضیات می یافتند. آن ها بین قانون های طبیعت و قانون های ریاضی شباهت هایی را احساس می کردند که اکنون یکی از پایه های اساسی علوم را تشکیل می دهد. بعدها یونانی ها در شناخت طبیعت پیشتر رفتند و اعتقاد استواری پیدا کردند که جهان بر اساس قانون های ریاضی طراحی شده و دستگاه کنترل شده ای است، از قانون هایی پیروی می کند و برای بشر قابل درک است.
دست آخر این که ریاضیات موسیقی ذهن است پس باید آن را نواخت.
. ریاضی و هنر
کم نیستند کسانی که ریاضیات را دانشی دشوار و دست نیافتنی و در ضمن خشک و خشن میپندارند و به همین مناسبت ، ریاضیدان و معلم ریاضی را فردی عبوس ، بی احساس و بی ذوق میپندارند و از اینکه کسی که سر و کار و رشته اش ریاضیات است، اهل ذوق و هنر و شعر و موسیقی باشد و از آن لذت ببرد، متحیر میشوند. آیا به واقع هنر و ریاضیات ، یا به عبارت دیگر ، زیبایی و ظرافت و ریاضی دو مقوله متضاد و دور از هم و ناسازگارند؟ آیا علاقه به ریاضیات و تخصص داشتن در آن ، به معنای بی ذوقی ، بی احساسی و دور بودن از زندگی است؟ انسان ترکیبی از احساس ، عاطفه و تاثیر پذیری از یک طرف و اندیشه و خرد و داوری منطقی از طرف دیگر است.در واقع انسان ، مجموع های یگانه از جان و خرد است. احساس و منطق را با هیچ نیرویی نمیتوان از هم جدا کرد. به قول هوشنگ ابتهاج عشق بیفرزانگی ، دیوانگی است. هر انسانی از تماشای چشم انداز یک دامنه سر سبز آرامش مییابد و در عین حال به فکر فرو میرود.شاعر احساس درونی خود را با شعر و نقاش با قلم و بوم بیان میکند. گیاه شناس در پی گیاه مورد نظر خود و زبان شناس در پی یافتن ریشه نامگذاری گیاه و داروشناس در جستجوی ویژگی های درمانی آن است و ریاضیدان نحوه قرار گرفتن برگ و گلبرگها یا اندازه ها و شکل ها را مورد مطالعه قرار میدهد. ولی هم گیاه عضوی یگانه است و هم انسان پس علت این گوناگونی در رابطه بین گیاه و انسان ، وجود جنبه های گوناگون و گسترده انسان و تجلی آنها در شرایط مختلفی است
● تاریخچه ارتباط ریاضیات و هنردر دوران رنسانس ، نقاشان بزرگ ، ریاضیدان هم بودند. آلبرتی (۱۴۷۲ - ۱۴۰۴) نخستین نیاز نقاش را هندسه میدانست. او بود که در سال ۱۴۳۵ میلادی ، اولین کتاب را درباره پرسپکتیو نوشت. نقاشان و هنرمندان برای جان دادن به تصویرها و القای فضای سه بعدی به آثار خود ، به ریاضیات روی آورند. بنابراین همه نقاشان دوره رنسانس نظیر آلبرتی ، دیودر ، لیوناردو داوینچی ، ریاضیدانانی هنرمند یا هنرمندانی ریاضیدان بودند. دزارک که خود ، معماری هنرمند بود به خاطر همین نیاز نقاشان و با اثبات قضیهای که به نام خود او معروف است، هندسه تصویری را بنیان نهاد و بعد از آن رفته رفته اصول بیشتری از ریاضیات تایید شد.
● چرا ریاضیات و هنر تا این اندازه به هم نزدیکند؟طبیعت ، سرچشمه زاینده و بی پایانی است برای انگیزه دادن به هنرمند و ریاضیدان. آنها از درون خود و از ایده ها سود میجویند و حقیقت را نه تنها آن گونه که مشاهده میشود، بلکه آن که باید باشد و آرزوی آدمی است، میبینند. هنر و ریاضیات هر دو کمال و ایده آل را میجویند.
● ریاضیات کلید طلایی برای زیبایی شناسی
طبیعت عنصر تقارن را عنوان نشانه زیبایی به هنرمند تلقین میکند و سپس ریاضیدان با کشف قانونمندیهای تقارن به مفاهیم شبه تقارن , تقارن لغزنده میرسد و کوبیسم را به هنرمند (نقاش ، شاعر یا موسیقیدان) تلقین میکند. نغمه ها و آواهای موجود در طبیعت الهام دهنده ترانه های هنرمندان بوده و ریاضیدانان با کشف قانونهای ریاضی حاکم بر این نغمه ها و تلاش در جهت تغییر و ترکیب آنها گونه های بسیار متفاوت و دل انگیزی در موسیقی آفریده اند. هر زمان که محاسبه درست ریاضی در نوشته های ادبی رعایت شده، آثار جالب و ماندگار و نزدیک به واقعیت و قابل قبول برای مخاطب خلق شده است. یکی از نمونه های این مساله رعایت توجه صحیح آندره یه ویچ در افسانه ثروتمند فقیر به محاسبات ریاضی در داستان خود میباشد (البته بدون وارد کردن محاسبات عددی) که آن را به اثری ماندگار و قابل پذیرش تبدیل کرده است. ترسیم های هندسی و نسبت زرین کمک شایانی به هنرمندان معمار و برج ساز و میکند.
● زیبایی ریاضیات در کجاست؟
در واقع تمامی عرصه ریاضیات سرشار از زیبایی و هنر است. زیبایی ریاضیات را می توان در شیوه بیان موضوع ، در طرز نوشتن و ارایه آن در استدلال های منطقی آن ، در رابطه آن با زندگی و واقعیت ، در سرگذشت پیدایش و تکامل آن و در خود موضوع ریاضیات مشاهده کرد. یکی از راه های شناخت زیبایی های ریاضیات (بخصوص هندسه) آگاهی بر نحوه پیشرفت و تکامل است. جنبه دیگری از زیبایی ریاضیات این است که با همه انتزاعی بودن خود ، بر همه دانش ها حکومت میکند و جز قانون های آن ، همچون ابزاری نیرومند دانشهای طبیعی و اجتماعی را صیقل میدهد، به پیش میبرد، تفسیر میکند و در خدمت انسان قرار میدهد.
● زیبایی مسایل ریاضی
برای بسیاری از مسایل ریاضی راه حلهای عادی وجود دارد که وقتی اینگونه مسایل را (با این روش ها) حل میکنید، هیچ احساس خاصی به شما دست نمیدهد و حتی ممکن است تکرار آن شما را کسل کند. ولی وقتی به مسال های برمی خورید که همچون دری مستحکم در برابر شما پایداری میکند و از هر سمتی به آن حمله میکنید ناکام میشوید زمانی که ناگهان جرقه های ذهن شما را روشن میکند عجب! پس اینطور! چه زیبا!و مساله حل میشود. در ریاضیات اغلب از اصطلاح زیباترین راه حل یا زیبایی راه حل استفاده میکنیم. ولی چرا یک راه حل مساله ما را تنها قانع و راضی میکند در حالی که دیگری شوق ما را برمی انگیزد و شجاعت فکر و ظرافت روش را آن موجب شگفتی ما میشود؟ راه حل زیبا باید تا حدی ما را به شگفتی وا دارد ولی تنها وجود یک جنبه نامتعارف و غیر عادی زیبایی استدلال ریاضی را روشن نمیکند، بلکه باید عینیت نیز داشته باشد.
همریختی نمونه با پدیده مورد نظر و سادگی درک نمونه و سادگی کار کردن با آن ، مفهوم عینی بودن را تشکیل میدهد. با بکار گرفتن عینیت ، زبان دشوار پدیده را به زبان ساده تر مدل عینی ترجمه میکنیم و نتایج لازم را بدست میآوریم.وقتی که دانش آموزی میخواهد به تنهایی مساله دشواری را حل کند نمونه عینی پدیدهای را باید در مساله شرح دهد، برای خودش بسازد، دشواری مساله های نامتعارف در این هست که برای حل آنها باید بطور مستقل نمونه همریخت (مساله هم ارز) را انتخاب کرد به نحوی که از پدیده نخستین ساده تر باشد. نامتعارف بودن این نمونه و نامنتظر بودن آن به معنای زیبایی و ظرافت راه حل است. زیبایی حل یک مساله را وقتی احساس میکنیم که به کمک یک نمونه عینی بدست آید و در ضمن نامنتظر باشد که بطور مستقیم به ذهن هر کسی نمیرسد و به زحمت در دسترس قرار میگیرد.
● رابطه زیباشناسی ریاضی
نامنتظر بودن + عینی بودن = زیبایی
این رابطه به فرهنگ ریاضی مربوط میشود و کسی که چنین فرهنگی دارد، دید گسترده تری دارد، با کمترین نشانه ها ، شباهت بین زمینه های مختلف ریاضی را پیدا میکند و به کشف رابطه بین آنها و فرمول بندی و استفاده از روابط گوناگون بین آنها می پردازد. و بدین ترتیب مساله را نامتعارف تر و زیباتر از بقیه حل میکند و با ساده ترین و کوتاه ترین و در عین حال جالب ترین روش به جواب مساله میرسد و موجب شگفتی و لذت خود و بقیه میگردد.
از کتاب " ریاضی وهنر" استاد پرویز شهریاری