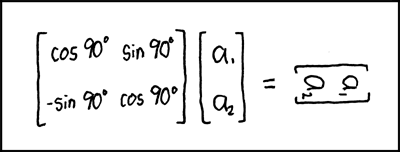. شعبده بازی ریاضی

شعبده بازی ریاضی

  جمع کردن اعداد چند رقمی در کمتر از ۱ ثانیه 

 شما می‌توانید قدرت خود را در محاسبه جمع اعداد چند رقمی به دوستان و یا دانش آموزان نشان دهید. اما اگر صبر کنید متوجه می‌شوید این کار چندان هم به قدرت محاسبه ریاضی شما بستگی ندارد. 

 از ۳ نفر بخواهید هر کدام  یک عدد سه ‌رقمی بگویند؛ این ۳ عدد را روی تابلو و  زیر همدیگر  بنویسید.

. بازی و ریاضی

بازی Quick Math

یک بازی محاسباتی برای دانش آموزان دبستان

برای رفتن به سایت بازی روی آیکن زیر کلیک کنید.

. شعبده بازی با ریاضیات

شعبده بازی با ریاضیات 

 در این جا ما می خواهیم با استفاده از چند عمل جمع و ضرب ساده یک غیب گویی انجام دهیم. 

 با دوستان خود دور یک میز بنشینید، ۵ جسم را روی میز قرار دهید به طوری که تعداد حرف های  تشکیل دهنده ی جسم ها از ۹ حرف بیش تر نبوده و هیچ کدام با هم مساوی نباشند. مانند کاغذ که ۴حرفی است و خودنویس که ۷ حرفی است.

. کاریکاتور ریاضی

بدون شرح!

. یک عدد جالب

  در مجموعه اعداد طبیعی عدد ۱۵۸۷۳ عدد عجیبی است. چون اگرآن را در هر رقمی ضرب (منظور از رقم، یعنی اعداد ۱ تا ۹ ) و سپس حاصل را در عدد ۷ ضرب کنیم ارقام عدد حاصل عبارت خواهد بود از رقم انتخابی، برای مثال اگر این عدد را در ۴ ضرب کنیم داریم: ۶۳۴۹۲=۴×۱۵۸۷۳ سپس با ضرب حاصل بدست آمده در ۷ داریم:

 ۴۴۴۴۴۴=۷×۶۳۴۹۲  

، حال شما برای ارقام دیگری نیز امتحان کنید .

. آیا می‌دانید

  آیا می‌دانید :

  اگر یک عدد دو رقمی را انتخاب کنید و سپس رقم‌های آن را از خود عدد دو رقمی کم کنید ، عدد بدست آمده همیشه مضربی از ۹ خواهد بود .
 مثال  ،  عدد  ۴۷  :     ۳۶ = ۷ - ۴ - ۴۷  

 در  اعداد ۳ رقمی اگر رقم‌های آن را از خود عدد سه رقمی کم کنید و سپس رقم‌های عدد بدست آمده را با هم جمع کنید ، همیشه جواب یا  ۹ خواهد بود یا  ۱۸ . 

 مثال  ،  عدد  ۷۲۳  :     ۷۱۱ = ۳ - ۲ - ۷ - ۷۲۳      ،      ۹ = ۱ + ۱ + ۷

 عدد ۶ به هر توان طبیعی که برسد ، رقم یکان حاصل  ۶  و  رقم دهگانش فرد است  و  نیز  رقم یکان نصف این عدد همیشه ۸ خواهد‌بود .

. ضرب سریع

 روش ضرب اعداد در عدد ۱۱

  روش تراختنبرگ برای ضرب اعداد مختلف در عدد یازده به صورت زیر است:

 ۱- آخرین عدد مضروب (عددی که در یازده ضرب می‌شود) را به عنوان رقم سمت راست جواب می‌نویسیم

 ۲- هر عدد متوالی از مضروب با همسایه طرف راست آن جمع می‌شود

 ۳- اولین عدد مضروب، رقم سمت چپ جواب می‌شود. این آخرین مرحله محاسبه‌است

. معمای ۱۳۸۵

 

 در این مقاله می‌خواهیم ببینیم که با استفاده از چهار عمل اصلی و رقم‌های سال ۱۳۸۵ چند تا از عددهای ۱ تا ۱۰۰ را می‌توانیم تولید کنیم ؟
 شرط کار این است که در رابطه‌هایی که برای تولید عددها می‌نویسیم :
 اولا" : از تمامی رقم‌های ۱۳۸۵یعنی {۱,۳,۸,۵} استفاده کنیم .
 ثانیا" : هیچ رقمی بیش از یک بار مورد استفاده قرار نگیرد .  

 مثلا" :                                        ۳ - ۵ - ۸ + ۱ = ۱   ،   (۱ + ۵)/(۳ × ۸) = ۴   ،   ۱۵- ۳۸ = ۲۳ .

. بازی ۴ رنگ

برای اینکه موضوع پست قبلی (قضیه ۴ رنگ) را بهتر درک کنید ، می‌توانید بازی زیر را دانلود کرده و سعی کنید که نقشه را با چهار رنگ، رنگ کنید. 

 حجم ۱۴۰ کیلوبایت  

  لینک دریافت

. یک عدد جالب ریاضی

 

 "۳۸۱۶۵۴۷۲۹"  این عدد نه رقمی را خوب نگاه کنید ، عدد جالبی است چرا که : در این عدد  کلیه‌ی ارقام از یک تا نه فقط یک بار آمده است . و خاصیت این است که : اگر از سمت چپ به راست در نظر بگیریم ،  دو رقم اول آن بر۲  و  سه رقم اول آن بر ۳  و  چهار رقم اول آن به عدد ۴  و  پنج رقم اول آن به عدد ۵  و .... بالاخره  نه رقم آن به عدد ۹  قابل قسمت است .
 خاصیت دیگر آن این است که : اگر رقم یک را حذف کنیم ، جمع هر دو رقم آن از چپ به راست برابر ۱۱ است . 

 منبع:نشریه‌علمی‌بامداد

. شگفتی اعداد

شگفتی اعداد 

 ۱۶ = ۴^۲ 

۱۱۵۶ = ۳۴^۲   

  ۱۱۱۵۵۶ = ۳۳۴^۲        

  ۱۱۱۱۵۵۵۶ = ۳۳۳۴^۲        

      ۱۱۱۱۱۵۵۵۵۶ = ۳۳۳۳۴^۲                 

        ۱۱۱۱۱۱۵۵۵۵۵۶ = ۳۳۳۳۳۴^۲                     

             ۱۱۱۱۱۱۱۵۵۵۵۵۵۶ = ۳۳۳۳۳۳۴^۲                              

 . 

 . 

.

. مسأله‌ی دلار گم‌شده

معما 

مسأله‌ی دلار گم‌شده

 سه‌دوست در یک رستوران ناهار می‌خورند و صورتحساب آن‌ها برابر با ۳۰ دلار می‌شود. آن‌ها توافق می‌کنند این مبلغ را به‌طور مساوی تقسیم و هریک ۱۰ دلار پرداخت کند.

 پیشخدمت صورتحساب و ۳۰ دلار پرداخت ‌شده را نزد صندوقدار می‌برد. صندوقدار تشخیص می‌دهد که اشتباه شده و صورتحساب درست تنها ۲۵ دلار است؛ بنابراین ۵ عدد ۱ دلاری را به پیشخدمت می‌دهد تا به مشتری‌ها برگرداند و از آن‌ها بابت این اشتباه عذرخواهی کند.

 در هر صورت پیشخدمت صادق نبوده و ۲ دلار را برای خود برداشته و تنها ۳ دلار را به مشتریان بر‌می‌گرداند. بنابراین هر یک از ۳ دوست ۹ دلار پرداخت کرده و پیشخدمت نیز ۲ دلار را دزدیده که جمع این مبالغ  ۲۹ دلار می‌شود؛ ولی صورت‌حساب اولیه ۳۰ دلار بود!

 دلار گم‌شده کجاست؟! 

 جواب