. کاربرد مثلث در موسیقی

 مثلث از ابتدایی‌ترین اشکال هندسی بوده که انسان‌ها در هنر از آن استفاده می‌کردند، بدون شک اولین نوع از انواع مثلث هم که در هنر از آن استفاده شده مثلث متساوی‌الاضلاع بوده‌است. اهرام مصر نمونه بسیاری قدیمی (حدود ۲۸۰۰ سال پیش از میلاد) از کاربری مثلت در هنر معماری قدیم بوده است. نمونه‌های دیگر از استفاده از مثلث در هنر تمدن‌های قدیم را می‌تواند در کاشی کاری‌های دیواره معابد در نپال نیز مشاهده ‌کرد.

 معروف هست تالس (۶۴۰-۵۵۰ سال پیش از میلاد) که پدر ریاضیات، نجوم و فلسفه یونان باستان بوده از شاگردان خود می‌خواهد که به مصر سفر کنند تا از پیشرفت علوم در آن تمدن اطلاعات لازم را کسب کنند و فیثاغورث (Pythagoras) از اولین افرادی بوده که این دستور را می‌پذیرد و به مصر سفر می‌کند. فیثاغورث از بنیانگذاران علمی موسیقی در جهان بوده و اغلب از هندسه برای مدل کردن استفاده می‌کرده، می‌خواهیم با استفاده از تجربیات او سلسه مطالبی را پیرامون ارتباط موسیقی با علوم هندسه، فیزیک و ریاضی آغاز کنیم.

 موسیقی را می‌توانیم به روش‌های مختلف مدل کنیم برای شروع کار ساده ترین روش را انتخاب می‌کنم که عبارت است از مدل‌کردن عمودی موسیقی یاهمان هارمونی. این روش مدل‌کردن به موسیقی‌دان‌ها کمک می‌کند تا هنگام فکر یا گوش کردن به هارمونی تصویر بهتری از نت‌های موسیقی داشته‌باشند بخصوص برای نوازندگان ساز غیر از پیانو.

 یک دایره در نظر بگیرید و آنرا به دوازده قسمت مساوی (یک اکتاو کروماتیک) تقسیم کنید و نت‌ها را به ترتیب روی هر قسمت بنویسید مانند شکل زیر. یکی از ساده‌ترین اشکال هندسی که در این دایره تقسیم شده می‌توان ساخت مثلت متساوی‌الاضلاع می‌باشد. که اگر آنرا بسازید و به آن دقت کنید تفسیر موسیقی آن یک آکورد افزوده خواهدبود. حتما” شنید که آکوردهای افزوده جدای از اینکه معکوس باشند یا نه چهار حالت بیشتر نیستند که دایره فوق این موضوع را بسادگی نمایش می‌دهد چرا که اگر راس بالایی مثلث را در جهت عقربه‌های ساعت حرکت دهیم تا رسیدن به نت E و انطباق دوباره روی خود، می‌تواند سه حالت دیگر را به خود بگیرد. همچنین به وضوح در شکل می‌توان دید که یک آکورد افزوده از سه فاصله (که در اینجا هرکدام یک ضلع مثلث هستند) یکسان معادل ۴ نیم پرده تشکیل شده‌است.

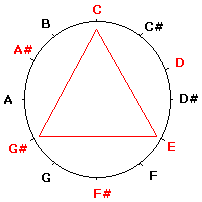
مثلث متساوی‌الاضلاع معادل یک آکورد افزوده

 شما باز هم می‌توانید مثلث‌های دیگری درست کنید. به شکل بعدی نگاه کنید که آکوردهای دو ماژور و لا مینور را نمایش می‌دهد. این دو مثلث (آکورد) خصوصیات جالبی دارند اولا” اضلاع آنها باهم برابر است، ثانیا” نسبت به خطی که از D کشیده می‌شود و به G# ختم می‌شود متقارن می‌باشند، حتما” می‌دانید که مینور نسبی گام دو ماژور، لامینور می‌باشد. به این طریق شما می‌توانید یک روش ساده برای پیدا کردن گام‌های مینور و ماژور نسبی پیدا کنید، هر چند این‌کار در پیانو بخاطر وضوح دیداری که چیدمان نت‌ها وجود دارد ساده می‌باشد.
 مثلث‌های متساوی‌الساقین هم جالب هستند یکی از آنها آکورد sus۲ را تشکیل می‌دهد که در شکل مشاهده می‌کنید و همچنین می‌توانید آکوردهای کاسته را نیز باز با یک مثلث متساوی‌الساقین درست کنید. اگر دقت کنید این مثلث متساوی‌الساقین حالت آکورد sus۲ برای C و حالت آکورد sus۴ برای G دارد. بنابر این می‌توان به ارتباط نزدیک آکوردهای sus> در حالت های ۲ و ۴ برای فاصله‌های پنجم با یکدیگر پی برد. این نکته هم جالب خواهدبود اگر شما راس D در این مثلث را نسبت به راس C قرینه کنید به آکورد sus۲ دیگری می‌رسید که یک پرده عقب تر است آکورد Csus۴ قرار دارد.

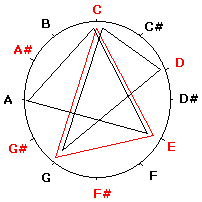
آکوردهای بزرگ، کوچک، sus۲ و sus۴

 شما می‌توانید دامنه مدل‌کردن را ادامه دهید و راجع به سایر مثلث‌ها فکر کنید، همچنین می‌توانید آکوردهای چهار صدایی را با انواع چهار ضلعی‌ها مدل کنید. سوالی که پیش می‌آید این است که آیا هستند افرادی که با شنیدن موسیقی این اشکال در ذهن آنها نقش ببندد؟ 

منبع:http://www.bedanid.com